Lösungsverfahren von linearen Gleichungen und linearen Gleichungssystemen mit einer oder zwei Variablen
Veröffentlicht am 11.10.2017
Gleichungssysteme nehmen nicht nur in der Mathematik sondern auch in anderen Schulfächern eine wichtige Rolle ein. Unter einer Gleichung wird in der Mathematik eine Aussage über die Gleichheit zweier Terme verstanden. die mit Hilfe des Gleichheitszeichens („=“) symbolisiert wird.
Dabei wird das mathematische Lösen von Gleichungen in höheren Klassenstufen als bekannt vorausgesetzt.
Beim Ausrechnen von Gleichungen beziehungsweise Gleichungssystemen wird bei
- einer vorhandenen Variablen eine mathematsche Aussage getroffen und
- werden bei zwei Variablen zwei mathematische Aussagen miteinander in Relation gesetzt,
um durch Lösungsverfahren (Aneinanderreihen von mathematischen Operationen) eine Lösungsmenge zu erhalten, die beim Einsetzen in die eine bzw. beide Gleichungen eine wahre Aussage ergibt.
Für das Lösen von Gleichungssystemen mit einer oder zwei Variablen gibt es die Lösungsverfahren:
- Äquivalenzumformung (Auflösen nach einer Variablen)
- Einsetzverfahren (oder Einsetzungsverfahren)
- Gleichsetzungsverfahren
- Additionsverfahren (auch als Eliminationsverfahren bezeichnet)
- Graphische Lösung
Bei Gleichungen mit mehr als zwei Variablen gibt es weitere Verfahren, welche teilweise auf den vorstehenden Lösungsansätzen aufbauen. Diese Lösungsverfahren werden in einem weiteren Blogeintrag beschrieben.
Generell muss bei allen Lösungsverfahren die gleiche Lösungsmenge bzw. das gleiche Ergebnis herauskommen, wenn man die gleiche Aufgabe als Ausgangsgleichung der Berechnung nimmt. Aus diesem Grund sind die aufgeführten Beispiele (bis auf die Äquivalenzumformung) von gleichen Aufgaben ausgehend.
-
Äquivalenzumformung bei linearen Gleichungssystemen
Die Äquivalenzumformung wird angewendet, wenn es in der Gleichung nur eine Variable gibt. Ziel ist es, die Gleichung durch mathematische Operationen so lange umzuformen, bis die Variable alleine auf der einen Seite und auf der anderen nur eine Zahl (ein Wert) steht.
Bei der Äquivalenzumformung ist ausschlaggebend, dass auf beiden Seiten der Gleichung genau dieselbe mathematische Operation durchgeführt wird, um die Gleichung in ihrer mathematischen Aussage nicht zu verändern.
Das Umformen von Gleichungen ist Grundlage und Bestandteil aller Lösungsverfahren.
Merke: Was man auf der linken Seite der Gleichung rechnet, muss man auch auf der rechten Seite der Gleichung rechnen!
Beispiel 1
3x + 7 = 22 | – 7
3x = 15 | : 3
x = 5
Beispiel 2
7 (4x – 2) = 14 | ()
28x – 14 = 14 | + 14
28x = 28 | : 28
x = 1
Beispiel 2:
2x(3x – 6) = 12x | () à Wer es sieht, kann auch gleich durch x teilen.
6x² – 12x = 12x | : x
6x – 12 = 12 | + 12
6x = 24 | : 6
x = 4
Tipps:
- Vorzeichen werden umgekehrt, in dem man die Gleichung mit (-1) multipliziert.
- Operatoren (Wurzel, Potenz, Logarithmus, …) werden immer mit der jeweiligen Gegenoperation aufgelöst.
- Um die einzelnen Operationen nachzuvollziehen, sollte immer aufgeführt werden, was im Folgeschritt gemacht wird (Beispiel „I +12“)
-
Einsetzverfahren (Einsetzungsverfahren)
Das Einsetzverfahren findet Anwendung, wenn zwei Gleichungssysteme mit zwei Variablen vorhanden sind. Ziel ist es, durch Äquivalenzumformung der einen Gleichung nach einer Variablen, diese in der anderen Gleichung einsetzen zu können, um so mit nur einer Variablen weiterzurechnen. Dabei werden immer wieder die gleichen Lösungsschritte abgearbeitet:
- Umformung der Gleichung A (B) nach einer Variablen.
- Einsetzen der umgeformten Gleichung in die andere (zweite) Gleichung.
- Umformen der zweiten Gleichung nach der noch vorhandenen Variablen.
- Einsetzen des Ergebnisses in die zuerst umgeformte Gleichung.
Beispiel 1 (Auflösen nach x)
I 8x – 4y = 8
II 0,5x + y = 3 | – 0,5x
II´ y = 3 – 0,5x | II´in I
I´ 8x – 4 · (3 – 0,5x) = 8 | ()
I´ 8x – 12 + 2x = 8 | +12
I´ 10x = 20 | : 10
x = 2 | x in I
I 8 · 2 – 4y = 8
I 16 – 4y = 8 | – 16
I -4y = -8 | : (-4)
y = 2
_____
L = {2;2}
Probe:
0,5 · 2 + 2 = 3
3 = 3 wahre Aussage
Beispiel 2 (Auflösen nach y)
I 2x + 8y = 5
II 2x – 3y = -6 | -2x
II´ -3y = -2x – 6 | : (-3)
II´ y = 2/3x + 2 | II´ in I
I´ 2x + 8 · (2/3x + 2) = 5 | ()
I´ 2x + 16/3x + 16 = 5 | – 16
I´ 22/3x = -11 | : 22/3
x = -1,5 | x in II
II 2 · (-1,5) – 3y = -6 | + 3
II -3y = -3 | : (-3)
y = 1
L = {-1,5;1}
Probe:
2 (-1,5) + 8 · 1 = 5
5 = 5 wahre Aussage
Tipps:
- Die Probe sollte immer in der Gleichung erfolgen, die das erste Variablenergebnis enthält.
- Veränderte Gleichungen sollten immer zur besseren Übersicht mit einer Fußzahl oder wie in dem Beispiel mit einem Strich versehen werden.
-
Gleichsetzungsverfahren
Das Gleichsetzungsverfahren wird angewandt, wenn zwei Gleichungssysteme mit zwei Variablen vorhanden sind. Ziel ist es, durch Äquivalenzumformung beide Gleichungen nach ein und derselben Variablen umzuformen, um dann die beiden Gleichungen gegenüberzustellen.
Dabei werden immer wieder die gleichen Lösungsschritte abgearbeitet:
- Beide Gleichungen nach der gleichen Variablen umformen.
- Gleichungen gegenüberstellen.
- „Neue“ Gleichung nach der noch enthaltenen Variablen auflösen.
- Einsetzen des Ergebnisses in eine der umgeformten Gleichungen.
- Zweite Variable berechnen.
Beispiel 1 (Gleichsetzen von x)
I 8x – 4y = 8 | + 4y
II 0,5x + y = 3 | – y
I´ 8x = 4y + 8 | : 8
II´ 0,5x = -y +3 | : 0,5
I´ x = 0,5y + 1
II´ x = -2y +6
à I´ und II´ gleichsetzen
0,5y + 1 = -2y + 6 | – 1
0,5y = -2y + 5 | +2y
2,5y = 5 | : 2
y = 2 | y in I
I 8x – 4 · 2 = 8 | + 8
8x = 16 | : 2
x = 2
____
L = {2;2}
Probe:
0,5 · 2 + 2 = 3
3 = 3 wahre Aussage
Beispiel 2 (Gleichsetzen von y)
I 2x + 8y = 5 | – 2x
II 2x – 3y = -6 | – 2x
I´ 8y = -2x + 5 | : 8
II´ -3y = -2x – 6 | : (-3)
I´ y = -1/4x + 0,625
II´ y = 2/3x + 2
à I´ und II´ gleichsetzen
-1/4x + 0,625 = 2/3x + 2 | – 2/3x
-2/3x – 1/4x + 0,625 = 2 | – 0,625 (0,625 = 5/8)
-11/12x = 11/8 | : (-11/12) oder · (-12/11)
x = -1,5 | x in I
2 · (-1,5) + 8y = 5 | + 3
8y = 8 | : 8
1 = 1
L = {-1,5;1}
Probe:
2 · (-1,5) + 8 · 1 = 5
5 = 5 wahre Aussage
Tipps:
- Vor dem Umstellen nach einer Variablen sollte geschaut werden, nach welchen Variablen es am besten geht. Hier gilt es – wo immer möglich – komplizierte Brüche und schwierige Dezimalzahlen zu vermeiden.
-
Additionsverfahren
Beim Additionsverfahren (auch Eliminationsverfahren genannt) wird durch Addition (Subtraktion) zweier Gleichungen eine Variable heraus gerechnet (eliminiert). Nach der nichteliminierten Variablen kann in Folge umgeformt werden.
Das Additionsverfahren benötigt ein weiteres Lösungsverfahren (in der Regel das Einsetzungsverfahren), um auch nach der im Schritt 1 eliminierten Variablen umzuformen.
Auch bei diesem Verfahren sind die vorgegebenen Lösungsschritte einzuhalten:
- Umformung der Gleichungen I (II) so, dass alle Variablen auf der linken (rechten) Seite und die Zahlen auf der anderen Seite stehen.
- Umformen der Gleichung I oder II so, dass eine Variable genau den gleichen Vorfaktor mit entgegengesetztem Vorzeichen (bei Anwendung der Addition) oder den gleichen Vorfaktor mit gleichem Vorzeichen (bei Anwendung der Subtraktion) erhält.
- Addieren (Subtrahieren) beider Gleichungen.
- Umformen der „neuen“ Gleichung nach der noch vorhandenen Variable.
- Einsetzen des Ergebnisses in eine der Ausgangsgleichungen.
Beispiel 1 (Eliminierung von x durch Addition)
I 8x – 4y = 8
II 0,5x + y = 3 | · (-16) (mal 2 bei II und geteilt durch 8 bei I wäre auch eine gangbare Lösung)
I 8x – 4y = 8 |
II´ -8x – 16y = -48 | I + II´ (8 und -8 sind die gleichen Vorfaktoren mit unterschiedlichem Vorzeichen)
-20y = -40 | : 20
y = 2 | y in I
I 8x – 4 · 2 = 8 | + 8
I 8x = 16 | : 2
x = 2
L = {2;2}
Probe:
0,5 · 2 + 2 = 3
3 = 3 wahre Aussage
Beispiel 2 (Eliminierung von y durch Subtraktion)
I 2x + 8y = 5 | · (-3)
II 2x – 3y = -6 | · 8
I´ -6x – 24y = -15 |
II´ 16x – 24y = -48 | I´- II´ (-24 und -24 sind die gleichen Vorfaktoren mit gleichem Vorzeichen)
-22x = 33 | : (-22)
x = -1,5 | x in I
I 2 · (-1,5) + 8y = 5 | + 3
8y = 8 | : 8
y = 1
L = {-1,5;1}
Probe:
2 (-1,5) + 8 · 1 = 5
5 = 5 wahre Aussage
Tipps:
- Vor dem Rechnen sollte man sich für eines von beiden Verfahren entscheiden. Ein Wechsel kann die Anzahl an Flüchtigkeitsfehlern erhöhen.
- Findet man das kleinste gemeinsame Vielfache (kgV) nicht, um die gleichen Vorfaktoren zu halten, einfach die zu eliminierenden Vorfaktoren miteinander multiplizieren. Eine einfache Erläuterung zum KgV findet man unter: https://de.wikipedia.org/wiki/Kleinstes_gemeinsames_Vielfaches.
-
Graphische Lösung
Bei der graphischen Lösung geht es darum, beide Gleichungen in einem Koordinatensystem darzustellen und den Schnittpunkt beider Graphen als Lösungsmenge abzulesen:
- Umformung der Gleichungen nach y
- Bestimmen zweier Punkte der Gleichungen I und II durch Einsetzen frei wählbarer Werte in x und Ausrechnen des y-Wertes
- Abtragen der Punkte (x/y) der Gleichungen I und II im Koordinatensystem
- Ablesen der Lösungsmenge (Schnittpunkt der Geraden I und II)
- Die Probe (falls verlangt) erfolgt durch Einsetzten des Schnittpunktes S in beiden Gleichungen.
- Der Beweis (falls verlangt) erfolgt durch rechnerisches Lösen.
- In der Regel endet die graphische Lösung mit einem einfachen Antwortsatz.
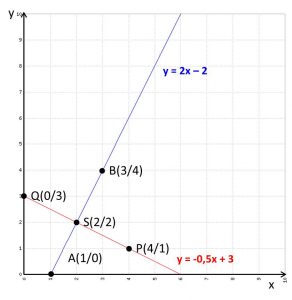
Beispiel
I 8x – 4y = 8 | -8x
-4y = -8 – 8 | : -4
y = 2x – 2
Punkt 1 (A)
y = 2x – 2 | x(1) = 1
y(1) = 2 · 1 – 2 = 0 à A(1/0)
Punkt 2 (B)
y = 2x – 2 | x(2) = 3
y(2) = 2 · 3 – 2 = 4 à B(3/4)
II 0,5x + y = 3 | – 0,5x
y = -0,5x + 3
Punkt 3 (P)
y = -0,5x + 3 | x(1) = 4
y(1) = -0,5 · 4 + 3 = 1 à P(4/1)
Punkt 4 (Q)
y = -0,5x + 3 | x(2) = 0
y(2) = -0,5 · 0 + 3 = 4 à Q(0/4)
Probe:
Gleichung I
8 · 2 – 4 · 2 = 8
8 = 8 wahre Aussage
Probe:
Gleichung II
0,5 · 2 + 2 = 3
2 = 2 wahre Aussage
Antwort: Der Schnittpunkt beider Geraden befindet sich im Punkt S (2/2).
Tipps:
- Das Koordinatensystem genau zeichnen. Achsen beschriften und Einteilung (1,2,3,..) genau abtragen.
- Beim Einsetzen und Verbinden der Punkte genau arbeiten. Kleine Abweichungen können zu einem verfälschten Ergebnis führen.
- Punkte immer eintragen und mit Großbuchstaben und Koordinaten bezeichnen.
- Die Graphen der Funktionen bezeichnen. Entweder mit der Funktionsgleichung in der Form y = ax + b (die Regel) oder mit I und II (die Ausnahme)
- Zur Sicherheit (auch wenn nicht verlangt) immer eine kurze Probe durchführen.
Von Andre Wiesener, unserem Konrektor für Nachhilfe in Koblenz.
Nutzen Sie unser kostenloses Beratungsgespräch!
Zum Kontaktformular