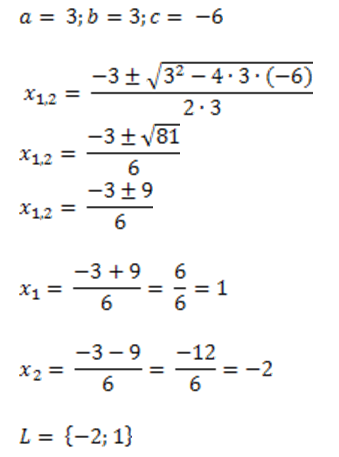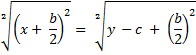Lösen von quadratischen Gleichungen

Veröffentlicht am 07.05.2018

Das Lösen von quadratischen Gleichungen nach verschiedenen mathematischen Lösungswegen gehört im heutigen Mathematikunterricht ab der Mittelstufe zum Handwerkzeug jedes Schülers und jeder Schülerin. In vorrangegangen Blogbeiträgen zum Thema: Lineare Gleichungen und Vereinfachen von Termen wurde Wissenswertes in Themenbereichen Termen und (linearen) Gleichungen dargestellt. Dieses hilft, um den Themenkomplex der quadratischen Gleichungen besser zu verstehen.

Bevor verschiedene Lösungsvarianten quadratischer Gleichungen beschrieben werden, ist die Frage zu klären: „Was ist eine quadratische Gleichung?“

Eine quadratische Gleichung ist eine Gleichung, welche die Form ax² + bx + c = 0 mit a ≠ 0 schreiben lässt oder durch Umformen in diese bringen lässt. Die höchste Potenzzahl ist hierbei immer „2“.

Die einzelnen Termglieder können anhand ihrer „Eigenschaften“ bezeichnet werden:

ax²     » quadratisches (bestimmendes) Glied
bx     » lineares Glied
c       » konstantes Glied

Häufig angewandte Lösungsschemen sind dabei:

1. Äquivalenzumformung (bei Sonderformen)
2. Lösungsformel für die allgemeine quadratische Gleichung („a-b-c-Formel“ oder auch „Mitternachtsformel“ genannt)
3. Lösungsformel für die quadratische Normalform (p-q-Formel)
4. Lösen mit Hilfe der quadratischen Ergänzung für die quadratische Normalform
5. Zerlegung in Linearfaktoren
6. Satz von Vieta

Um auswählen zu können, welche Formel oder welcher Lösungsweg am sinnvollsten ist, müssen einige Formen von quadratischen Gleichungen näher erläutert werden.

Formen von quadratischen Gleichungen (wichtige Beispiele)

Allgemeine quadratische Gleichung

ax² + bx + c = 0
Bsp. 3x² + 3x – 6 = 0

Quadratische Normalform

x² + bx + c = 0 oder x² + px + q = 0
Bsp. x² + x – 2 = 0

Fehlendes lineares Glied

ax² + c = 0
Bsp. 2x² – 8 = 0

Fehlendes konstantes Glied

ax² + x = 0
Bsp. 2x² – 8x = 0

Gleichung in Scheitelpunktform

a(x – d)² + e = 0
Bsp. 3(x – 4)² + 3 = 0

Für jede dieser Formen gibt es allgemeine oder spezielle Lösungsansätze. Vielfach geben aber auch die Aufgabenstellungen die Lösungswege vor. Es ist daher am besten, sich mit allen Lösungsverfahren auszukennen.

Lösungsverfahren

 Beim Lösen von quadratischen Gleichungen ist es wichtig zu erkennen, ob eine quadratische Gleichung

• eine Lösung (Ausnahmefall)
• keine Lösungen (Widerleg der Gleichung)
• zwei Lösungen (Normalfall)

hat.

Hierzu sind folgende Aussagen immer zu beachten.

• Eine lösbare Quadratwurzel hat immer genau eine Lösung, wenn der Radikand (Zahl unter den Wurzelzeichen) = 0 ist.

x_1,2 = √0
x = 0; denn: 0 · 0 = 0

• Eine lösbare Quadratwurzel hat immer zwei Lösungen, eine mit positiven Vorzeichen und eine mit negativen Vorzeichen, wenn der Radikand > 0 ist.

x_1,2 = √4
x₁ = +2; denn: (+2) · (+2) = 4
x₂ = – 2; denn: (- 2) · (-2) = 4

• Eine lösbare Quadratwurzel hat immer keine Lösung, wenn der Radikand < 0 ist.

 x_1,2 = √(-4) » nicht lösbar, da es kein Zahl gibt, die mit sich selbst multipliziert = (-4) ergibt.

Äquivalenzumformung (bei Sonderformen)

• Fehlendes lineares Glied (ax² + c = 0)

Lösungsformel:

Musterbeispiel: 2x² – 8 = 0

x1 = -2
x2 = 2

• Fehlendes konstantes Glied (ax² + bx = 0)

Durch Ausklammern von x ergibt sich die umgeformte Gleichung x · (ax + b) = 0. Damit ist x₁ = 0, denn alles multipliziert mit „0“ ergibt „0“. Bestimmt werden muss jetzt nur noch x₂, also der Klammerwert ax + b = 0.

Lösungsformel

x1 = 0
x2= -b/a

Musterbeispiel: 2x² – 8x = 0

x1 = 0
x2 = – (-8)/2 = 4
L = {0; 4}

Lösungsformel für allgemeine quadratische Gleichungen

(ax² + bx + c = 0)

Lösungsformel: a-b-c-Formel (Mitternachtsformel)

Musterbeispiel: 3x² + 3x – 6 = 0

Lösungsformel für quadratische Normalformen

(x² + px + q = 0 oder ax² + bx + c = 0 mit a = 1)

Lösungsformel: pq-Formel

Musterbeispiel: x² + x – 2 = 0

Hinweis 1:
Bevor man die pq-Formel anwenden kann, muss man die Gleichung so umformen, dass der Vorfaktor von x² = 1 ist. Am einfachsten geht dieses durch Dividieren durch den Vorfaktor.

3x² + 3x – 6 = 0  I ÷3
x² + x – 2 = 0

Hinweis 2:
Jede Gleichung der quadratischen Normalform kann mit der a-b-c-Formel (Mitternachtsformel) gelöst werden. Dabei ist a = 1.

Lösen mit Hilfe der quadratischen Ergänzung

(x² + px + q = y oder ax² + bx + c = y mit a = 1)

Um diesen Lösungsansatz besser nachzuvollziehen, sollte man sich mit der 1. und 2. binomischen Formel etwas auskennen. Die Idee, welche hinter der quadratischen Ergänzung steht, ist mit Hilfe des Wurzelziehens zwei lineare Gleichungen zu erzeugen.

Ansatz: 1. Binomische Formel

Ansatz: 2. Binomische Formel

Lösungsansatz bei y = 0 (auch durch vorheriges Umformen möglich):

Musterbeispiel: x² + x – 2 = 0
b = 1; c = -2; y = o

Aus der Wurzel auf der linken Seite der Gleichung ergeben sich die Lösungsmöglichkeiten „+1,5“ und „-1,5“. Auf der rechten Seite der Gleichung heben sich Quadratwurzel und Potenzzahl „2“ auf. Da auf der linken Seite durch die Wurzel zwei Lösungsmöglichkeiten entstehen, ergeben sich auch für „x“ zwei Lösungsmöglichkeiten.

Lösungsansatz bei y ≠ 0:

Musterbeispiel: 3x² – 3x – 70 = 20

Hinweis 1:
Das Lösen mit der quadratischen Ergänzung ist nicht darauf angewiesen, dass y = 0 ist. Es sind also generell beide Lösungsansätze möglich.

Hinweis 2:
Bevor man den Lösungsansatz der quadratischen Ergänzung anwenden kann, muss man die Gleichung so umformen, dass der Vorfaktor von x² = 1 ist.

Zerlegung in Linearfaktoren

Für allgemeine Formen der quadratischen Gleichung (ax² + bx + c = 0) unter Berechnung von x₁ und x₂ über die a-b-c-Formel.

Lösungsform:

ax² + bx + c = a • (x – x1) • (x -x2)

Musterbeispiel: x² + x – 2 = 0  und L = {-2;1}

3x² + 3x -6 = 3 • (x – 1) • (x – (-2))
3x² + 3x -6 = 3 • (x – 1) • (x +2)

Für quadratische Normalformen der quadratischen Gleichung (x² + px + q = 0) unter Berechnung von x₁ und x₂ über die pq-Formel.

Lösungsform:

x² + px – q = (x – x1) • (x – x2)

Musterbeispiel: x² + x – 2 = 0 und L = {-2;1}

x² + x – 2 = (x – 1) • (x – (-2))
x² + x – 2 = (x – 1) • (x + 2)

und

für nicht nominierte Polynome (allgemeine Form: ax² + bx + c = 0) unter Berechnung von x₁ und x₂ über die a-b-c-Formel

Lösungsform:

ax² + bx + c = a • (x – x1) • (x – x2)

Beispiel:

3x² + 3x + 6 = a • (x – 1) • (x – 2)

Hinweis 1:

Das Zerlegen in Linearfaktoren stellt kein eigenes Lösungsverfahren dar. Die Linearfaktoren können durch bekannte Lösungsverfahren wie pq-Formel und abc-Formel herausgebildet werden.

Kleine (unmathematische) Eselsbrücke: Linearfaktoren ergeben sich aus der Lösungsmenge der Variablen „x“ und des „Gegenteils“ (Gegenzahl) von x₁ oder x₂.

x₁ = + 2 » Linearfaktor = (x – 2)
x₂ = – 3 » Linearfaktor = (x + 3)

Hinweis 2:
Sind die Linearfaktoren bekannt oder gegeben, kann anhand der obigen Lösungsschemen durch Ausmultiplizieren eine quadratische Gleichung der allgemeinen oder der Normalform gebildet werden.

(x + 3) · (x – 2) = 0
x² + 3x – 2x – 6 = 0
x² + x – 6 = 0

2 · (x + 3) · (x – 2) = 0
2 · (x² + 3x – 2x – 6) = 0
2 · (x² + x – 6) = 0
2x² + 2x – 12 = 0

Satz von Vieta für die quadratische Normalform

(x² + px + q = 0 oder ax² + bx + c = 0 mit a = 1)

Ist eine quadratische Gleichung in Normalform (x² + px + q = 0), so gilt:

0 = x² + px + q = (x – x1) • (x – x2) = x² – (x1 + x2) • x + x1 • x2

Daraus ergibt sich die Lösungsformel:

-p = x1 + x2
und
q = x1 + x2

Musterbeispiel: x² + x – 2 = 0

p = 1; q = -2

-1 = x1 + x2     -2 = x1 • x2

Durch Probieren und Umformung erhält man Zahlenpaare x₁ und x_2, für welche die obige Vorschrift gilt. Hierbei empfiehlt es sich, sich auf x₁ als Ausgangszahl zu konzentrieren und im Wechsel Zahl und Gegenzahl einzusetzen.

1. Einsetzen x₁ = 1
   -1 = 1 + x2
   -2 = x2

2. Einsetzen x₂ in Gegengleichung
   -2 = x1 • (-2)
   1 = x1

L = {-2; 1}

Der Vorgang muss solange wiederholt werden, bis x₁ und x₂ in beiden Gleichungen eine wahre Aussage ergeben.

Hinweis 1:

Das Satz von Vieta eignet sich, wenn sich die Lösungen für p und q im Bereich der Menge der ganzen Zahlen befinden.

FAZIT:

Es gibt vielfältige Lösungsmöglichkeiten, quadratische Gleichungen zu Lösen. Voraussetzung ist jedoch, die Grundlagen unter anderem der Potenz- und Wurzelgesetze und der binomischen Formeln zu kennen. Wer sich ein wenig übt und die Lösungsschritte und Voraussetzungen der Lösungsansätze beherrscht, wird mit dem Lösen von quadratischen Gleichungen wenig Probleme haben.

 

Von Andre Wiesener, unserem Konrektor für Nachhilfe in Koblenz.